Dynamic Programming-1

Understanding Dynamic Programming-1

The twin keys to understanding Dynamic Programming are

Optimal Solutions are made up of optimal solutions to sub problems. This might seem obviously true but it isn't. Take the case of the Travelling Salesman problem. Picking the shortest path from A to B need not result in an optimal tour. There are other cases where the optimal sub problem rule applies. The generation of Fibonacci Numbers for instance.
Fib(n) = Fib(n-1) + Fib(n-2) an actual instance will be
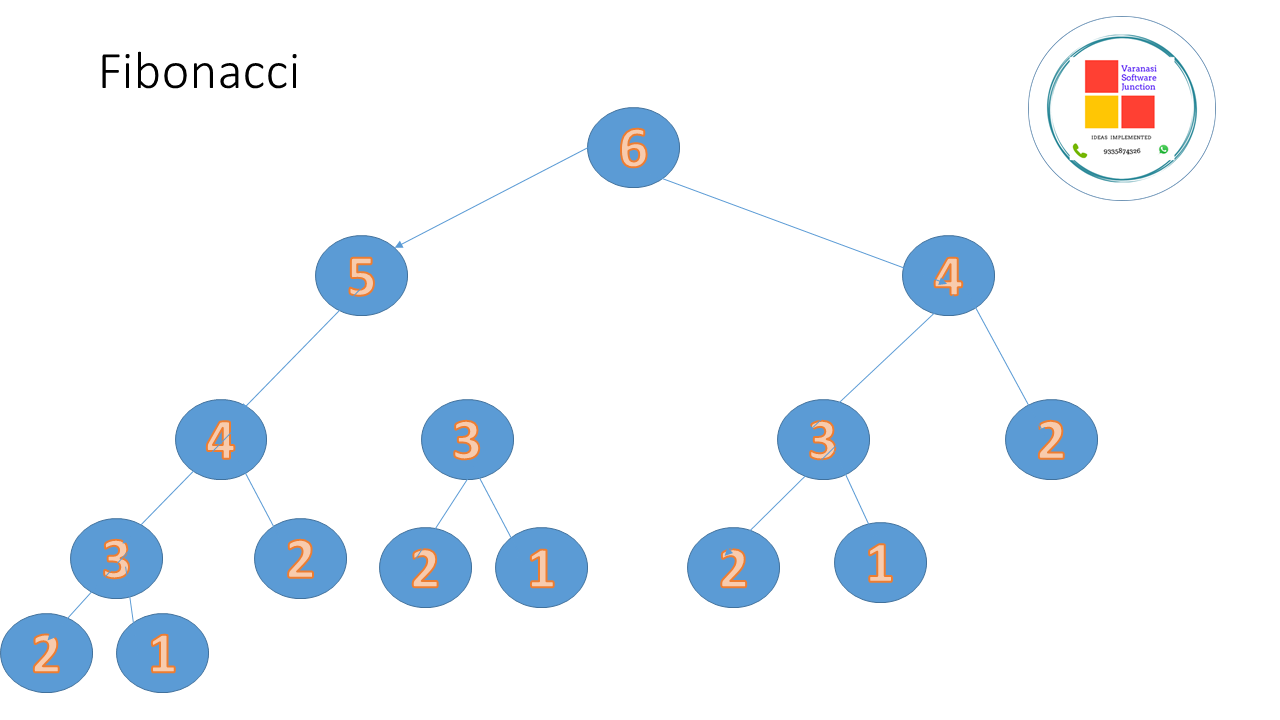
Fib(6)=Fib(5) + Fib(4). Now, we have a method for evaluating Fib(5) and Fib(4) but if you happen to discover a more optimized version you can simply replace the previous call.
The second is Memoization. What is Memoization? It simply means storing the intermediate results so that they are not calculated over and over again. Look up this diagram:

The call for Fib(3) is repeated thrice.

Let us implement this without memoization and with memoization.

Code





def fib(n):#Fib without DP
    global count
    count += 1
    if n == 1:
        return 0
    if n == 2:
        return 1
    return fib(n - 1) + fib(n - 2)


def dpFib(n):#Fib with DP
    global count
    global fibs
    count += 1
    if fibs.get(n) is None:
        fibs[n] = dpFib(n - 1) + dpFib(n - 2)  # Memoize
    return fibs[n]


fibs = {}

count = 0
result = fib(6)
print("Fib(6) without Memoization ", result, ", count=", count)
count = 0
fibs = {1: 0, 2: 1}
result = dpFib(6)
print("Fib(6) with Memoization ", result, ", count=", count)
print("Dictionary as memo ", fibs)

Output




C:\Users\Lenovo\AppData\Local\Microsoft\WindowsApps\python3.10.exe C:/pythoncodecamp/dynamicprogramming/fibonacci.py
Fib(6) without Memoization  5 , count= 15
Fib(6) with Memoization  5 , count= 9
Dictionary as memo  {1: 0, 2: 1, 3: 1, 4: 2, 5: 3, 6: 5}

Process finished with exit code 0