How to check if a given number is a Disarium number using Python?

What is a Disarium number?

(This is a question that is asked often in Coding Interviews and also in programming assignments in schools and college courses)

A Disarium number is a number where the sum of digits raised to powers equal to their position gives back the number.

Example

135 has the 3 digits 1, 3 and 5. 1 is at position 1,  3 at position 2 and 5 at position 3.
So, the sum will be 1¹ + 3² + 5³=1 + 9 + 125 = 135. So, this is a Disarium number.

Let us try with 123

sum =1¹ + 2² + 3³=1 + 4 + 27=32
14 is not equal to 123 so this is not a Disarium number

The first thing to do is to separate the digits of the number.

We will use the two operators // and % 
// is integer division. For example 123 divide by 10 is 12.3, 123 integer divide by 10 will give 12 since .3 will be ignored.

123/10 =12.3

123//10 =12

What does % do. It gives the remainder. Thus 123 % 10=3, 

How does it help in finding the digits. Consider this sequence.

n=123

r= n % 10  = 3

n=n//10      = 12

r=n % 10   = 2

n=n//10      =1

r=n % 10   =1

n=n//10      =0

This gives us the following program.

n=123

while n!=0:

    r=n%10

    n=n//10

    print(r)

Next step, we need to get the position of each digit. How shall we get that?

Let us add a counter to the loop.

n=123

count=0

while n!=0:

    r=n%10

    n=n//10

    count+=1

    print("Digit = ",r, ", Position = ", count)

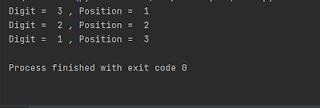
The positions are in reverse order. To get it in proper order let us subtract the positions from 4, that is from 1 more than the position.

n=123

count=0

length=len(str(n)) + 1

while n!=0:

    r=n%10

    n=n//10

    count+=1

    position=length-count

    print("Digit = ",r, ", Position = ", position)

We can complete the program now.

n=123

copy = n

count=0

sum=0

length=len(str(n)) + 1

while n!=0:

    r=n%10

    n=n//10

    count+=1

    position=length-count

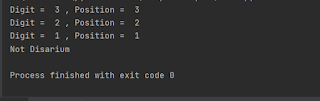
    sum = sum + r ** position

    print("Digit = ",r, ", Position = ", position)

if sum==copy:

    print("Disarium")

else:

    print("Not Disarium")

Change n=135

Contact us for Python Classes in Varanasi for offline classes and online classes in other places. 

Contact Us on this form